Kiedy nauczono sieć pamiętać, czyli dwa słowa o LSTM’ach

Bartosz Puszkarski
Zdjęcie autorstwa Pixabay z Pexels: https://www.pexels.com/pl-pl/zdjecie/na-zewnatrz-ulozone-kamienie-289586/

Co znajdziesz w tym artykule:

  • Czym są Rekurencyjne Sieci Neuronowe?
  • Czym jest LSTM i jak działa?
  • Dlaczego LSTM jest tak popularny?

Everything goes, everything comes back; eternally rolls the wheel of being.

„Thus Spoke Zarathustra”, Friedrich Nietzsche

Czym są Rekurencyjne Sieci Neuronowe?

W skrócie, są to wszelkie sieci neuronowe, których wewnętrzna architektura opiera się na sprzężeniu zwrotnym w przepływie informacji.

Jasne, da się prościej!
Każda informacja, która wychodzi z sieci trafia jako część danych wejściowych w następnej iteracji.

Przydałby się przykład, więc proszę bardzo:
Wyobraź sobie, że uczysz się gotować. Twoim celem jest na podstawie dostępnych składników wyprodukować potrawę, która będzie smakowała osobie jedzącej. Po tym jak osoba spróbuje twojej potrawy wyraża opinię, w której ocenia jak świetnie Ci to wyszło. W takim wypadku:

  • Składniki = dane wejściowe,
  • Ty i proces gotowania = sieć neuronowa,
  • Ocena osoby próbującej = wynik.

No tak, ale skoro ktoś już zjadł to, co przygotowałem, jaki ma sens to całe sprzężenie zwrotne? Otóż wpływa ono na twoje przyszłe gotowanie! Jeżeli osoba, która spróbowała twoich kulinarnych eksperymentów stwierdzi, że są pyszne, będziesz dalej kontynuował proces gotowania w taki sposób, jak robiłeś to do tej pory. Jednak jeżeli usłyszysz: „No, za słone” to będziesz pamiętał o tym przy przygotowywaniu następnego posiłku, tym samym opinia stanie się częścią twoich danych wejściowych!

Rekurencyjne sieci neuronowe mają jednak jedną istotną wadę wpływającą na ich możliwości wydajnościowe – zjawisko zanikającego gradientu. W dużym uproszczeniu, zanikający gradient to zjawisko związane z długością treningu i przyrostem danych, gdzie wagi podczas treningu nie są aktualizowane wtedy, kiedy powinny.
Aby zwizualizować to na naszym przykładzie kulinarnym, wyobraźmy sobie sytuację, w której ugotowałeś 100 „zbyt słonych” potraw i 101 jest również zbyt słona! ale z powodu zanikającego gradientu zmiana wag sieci może być zbyt mała, aby mieć jakikolwiek wpływ na wydajność, a zatem nie pozwala sieci na prawidłowe uczenie się.

Czym jest LSTM?

Long-Short Term Memory to mechanizm opracowany przez Seppa Hochreitera i Jürgena Schmidhubera opublikowany w Dzienniku „Neural Computation” w 1997 roku. Widać więc, że nie jest to wcale najmłodsza architektura. Została zaprojektowana specjalnie z myślą o rozwiązaniu problemu zanikającego gradientu. Jej główny założeniem jest przekazywanie stanu sieci w dwóch osobnych wektorach reprezentujących pamięć specyficzną dla danej komórki c(t) oraz pamięć długoterminową h(t) nazywaną też stanem ukrytym (hidden state). Reprezentacja graficzna została zaprezentowana na poniższym obrazku. Zwyczajowo, h(t) traktuje się także jako wyjście z sieci.

Pojedyncza komórka LSTM

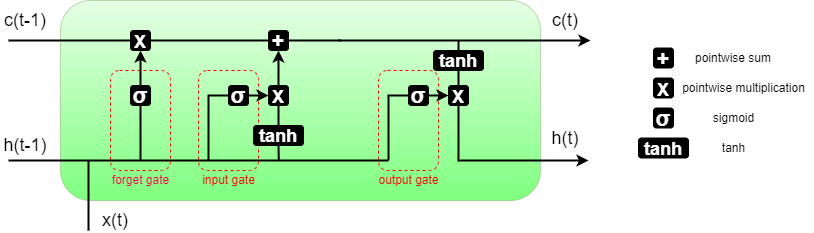
Pojedyncze komórki możemy łączyć ze sobą, tworząc wielowarstwowy LSTM. Jest to najpopularniejsze podejście, gdyż jedna komórka sama w sobie posiada ograniczone możliwości zarówno wykrywania nowych zależności jak i optymalizacji tych już wyuczonych. Ilość komórek w naszym LSTM nazywamy ilością warstw (oznaczane najczęściej num_layers) i jest podstawą do wyznaczania kształtu wektorów wag i pamięci.

Jak wyglądają wnętrzności LSTM?

Zacznijmy od matmy, która to wszystko opisuje. Nie martw się, jeżeli równania wyglądają strasznie, w dalszej części artykułu każde z nich objaśnię i powiążę ze wcześniejszym rysunkiem, dzięki czemu cały koncept stanie się bardziej przyjazny. No to zapinamy pasy…

Kadr z filmu Kac Vegas

Pierwszym krokiem jest inicjalizacja stanu początkowego, czyli wygenerowanie nowych wektorów c oraz h o wymiarach (D∗num_layers,H_out​) gdzie D to parametr równy 1 dla standardowego LSTM i 2 dla LSTM dwukierunkowego, num_layers to ilość warstw i H_out to oczekiwany rozmiar wyjściowy. Domyślnie wypełniamy wektory początkowe zerami.

Równania przedstawiają operacje krok po kroku czytając graf architektury od lewej do prawej. Są one opisem realizowanych operacji w sposób sekwencyjny. Podstawowymi danymi, które posiadamy przed przystąpieniem do obliczania równań są: c(t-1), h(t-1), x(t) gdzie dwa pierwsze zostały wyjaśnione w poprzednim akapicie, a x(t) jest wektorem danych wejściowych w iteracji t. Dla pierwszej iteracji t=1 wektory c(t-1) oraz h(t-1) są wektorami początkowymi, zerowymi. Wszystkie macierze W oraz U reprezentują wagi na poszczególnych bramkach.

(1)   \begin{equation*} f_t = \sigma(W_fx_t + U_fh_{(t-1)}) \end{equation*}

(2)   \begin{equation*} i_t = \sigma(W_ix_t + U_ih_{(t-1)}) \end{equation*}

(3)   \begin{equation*} o_t = \sigma(W_ox_t + U_oh_{(t-1)}) \end{equation*}

(4)   \begin{equation*} c'_t = \tanh(W_cx_t + U_ch_{(t-1)}) \end{equation*}

(5)   \begin{equation*} c_t = f_t*c_{t-1} + i_t * c'_t \end{equation*}

(6)   \begin{equation*} h_t = \tanh{(c_t)}* o_t \end{equation*}

Wewnątrz komórki wyróżniamy 3 bramki:

  • Bramka „zapomnij” (forget gate) – Przedstawiona na równaniu 1, oznaczona f_t. Kolejno wykonywane jest na niej przemnożenie wektora danych przez wagi oraz wektora pamięci długotrwałej przez powiązane wagi. Następnie na zsumowanym wyniku stosowana jest sigmoidalna funkcja aktywacji. Jej celem jest sprawdzenie, czy nowe dane mają istotny wpływ na całość i ewentualne spowodowanie „zapomnienia” aktualnego stanu komórki. W jaki sposób jest to robione? Otóż wynik bramki „zapomnij” jest mnożony później bezpośrednio z wektorem c(t) reprezentującym stan komórki. Dzięki temu, jeżeli na wyjściu z funkcji sigmoidalnej mamy wektor wypełniony zerami, nasz cell state także zostanie wyzerowany.
  • Bramka „wejście” (input gate) – Przedstawiona na równaniu 2, oznaczona i_t. Wykonywane są te same operacje co na bramce zapomnij z wykorzystaniem adekwatnych dla bramki macierzy wag W oraz U. Cel tej bramki to zdecydowanie jaka nowa informacja jest na tyle istotna, aby powinna zostać dodana do stanu komórki.
  • Bramka „wyjście” (output gate) – Przedstawiona na równaniu 2, oznaczona o_t. Wykonywane są te same operacje co na bramce zapomnij z wykorzystaniem adekwatnych dla bramki macierzy wag W oraz U. Jej cel to zdecydowanie jakie informacje są na tyle istotne, aby formować nowy stan ukryty sieci. Jej decyzja wpływa na dalsze uaktualnienie stanu ukrytego sieci stanem danej komórki.

To chyba nie było takie złe, co? To lecimy dalej.

Przy każdej bramce widzimy dodatkowe operacje, które wpływają na całokształt działania.
Pierwszym z takich elementów, ulokowanym bezpośrednio nad bramką forget, jest zwykła operacja mnożenia, która została opisana w akapicie poświęconym bramce „zapomnij”.

Kolejna sekcja, ulokowana za bramką „wejście” nazywana jest często w literaturze siecią nowej pamięci. To ta część na podstawie decyzji bramki wejścia tworzy nowy wektor informacji, która powinna zostać dodana do stanu komórki. Równanie obliczające wektor, który powinien zostać dodany do stanu komórki jest zaprezentowane jako równanie nr 4. Wykorzystujemy tam funkcję tanh obliczoną na sumie wymnożonych macierzy wag i wektorów stanu ukrytego oraz danych wejściowych. Następnie wynik operacji tanh jest mnożony przez wynik bramki i_t, dzięki czemu zachowujemy jedynie istotną informację, a potem sumowany ze stanem komórki. Tę ostatnią część opisuje równanie nr 5.

Ostatnią sekcją jest część aktualizująca stan ukryty. Przedstawia ją równanie nr 6. Tutaj stan komórki otrzymany w poprzednim kroku przechodzi przez funkcję tanh a następnie jest wymnażany z wynikiem otrzymanym z bramki „wyjście”. Dzięki temu, stan ukryty sieci jest uaktualniany jedynie o informację, która wywiera istotny wpływ na otrzymywany wynik i jej funkcjonowanie.

I to by było na tyle!

Dlaczego LSTM jest taki popularny?

Dzięki swoim cechom, LSTM jest jednym z pierwszych rozwiązań, które w skuteczny sposób radziło sobie z przeszkodą w postaci zanikającego gradientu, co pozwoliło na efektywne wykorzystanie modelu w problemach o dużym przepływie danych, takich jak Przetwarzanie Tekstu Naturalnego – dobrze opisany przykład z kodem.

Jako sieć rekurencyjna, LSTM nadaje się do wykrywania, klasyfikacji lub regresji wszelkich cyklicznych i powtarzalnych danych. Analiza szeregów czasowych jest także zagadnieniem, które często przewija się w przykładach wykorzystania tej architektury – kolejny przyjemny przykład. Do szeregów czasowych wliczamy zachowanie giełdy, przewidywanie temperatury, przewidywanie wilgotności, aktywność użytkowników.

Analiza EKG jest jednym z możliwych zastosowań LSTM i innych sieci rekurencyjnych w domenie związanej z medycyną. Sieci rekurencyjne odnoszą tutaj znaczące sukcesy, chociaż ze względu na tempo ich działania zaczynają być zastępowane przez nowsze rozwiązania. Dla zainteresowanych jednak podzielę linkiem do własne j publikacji, która uwzględnia LSTM w klasyfikacji chorób serca na podstawie EKG, a tutaj można znaleźć przykład kodu, który został wykorzystany w badaniach.

Podsumowanie

W tym artykule krótko scharakteryzowałem czym są sieci rekurencyjne oraz wytłumaczyliśmy ich działanie na lekkim przykładzie. Następnie zagłębiliśmy się w podstawowe założenia LSTM oraz wyjaśniliśmy równania, jakie stanowią jego serce. Na koniec przytoczone zostały przykłady użycia.

Mam nadzieję, że teraz LSTM nie jest Ci już straszny, a wszystkie jego bramki stoją przed tobą otworem. Zachęcam do dzielenia się opinią o artykule lub wszelkimi pytaniami w komentarzach.

Źródła:
https://doi.org/10.1162/neco.1997.9.8.1735
https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html,
https://towardsdatascience.com/recurrent-neural-networks-deep-learning-for-nlp-37baa188aef5
https://iopscience.iop.org/article/10.1088/1361-6579/ac6e55
https://machinelearningmastery.com/time-series-prediction-lstm-recurrent-neural-networks-python-keras/

Related Posts